問題
\(\theta\)は実数とする. \(xyz\)空間の2点\(A(0,0,\frac{\sqrt{2}}{4}), P(\cos{\theta},\sin{\theta},\frac{1}{2}\cos{\theta})\)を通る直線\(AP\)が\(xy\)平面と交わるとき, その交点を\(Q\)とする. \(\theta\)が\(-\frac{\pi}{4}<\theta <\frac{\pi}{4}\)の範囲を動くときの点\(Q\)の軌跡を求め, その軌跡を\(xy\)平面上に図示せよ.
方針
まずは点\(Q\)の座標を求めるために、直線\(AP\)をベクトル方程式による媒介変数表示で求める。
その後\(z\)座標が\(0\)という条件から\(t\)を消去し、\(Q\)の\(x\)座標、\(y\)座標を求める。
この際\(x\)座標、\(y\)座標がともに\(\sin{\theta},\cos{\theta}\)を用いて表されることから、極座標を用いて軌跡を考えることが出来ないかという発想に持っていく。
解答

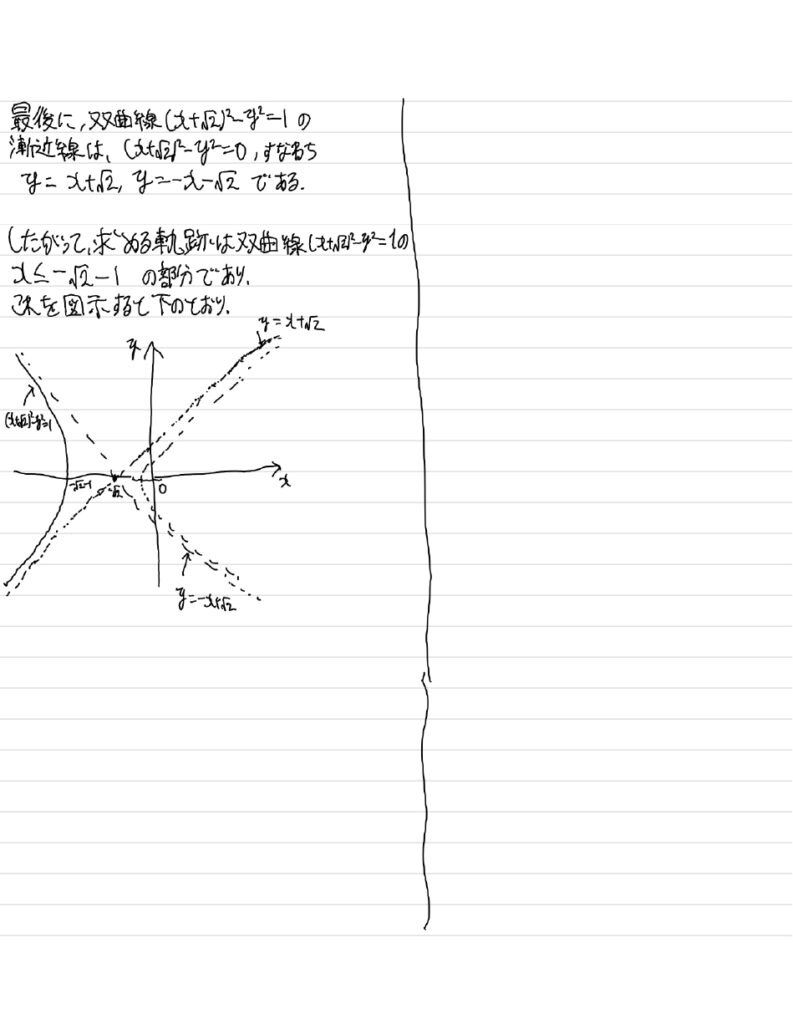
補足
最後の図示のところで曲線の形が歪になってしまい申し訳ないです…

