Ⅲ
問題
座標平面において円 \((x-1)^2+(y-1)^2=1\) を \(C\) とする。\(a\) を \(1\) より大きい実数とし, \(2\) 点 \(A(2a, 0)\), \(B(-a, 0)\) をとる。点 \(A\) を通る円 \(C\) の \(2\) 本の接線のうち傾きが小さい方を \(l_1\) とし, 点 \(B\) を通る円 \(C\) の\(2\) 本の接線のうち傾きが大きい方を \(l_2\) とする。\(l_1\) と \(l_2\) の交点を \(D\) とする。
(1)直線 \(l_1\) の方程式を \(a\) を用いて表せ。
(2)点 \(D\) から \(x\) 軸へ下した垂線と \(x\)軸の交点を \(H\) とする。△\(BDH\) と △\(ADH\)の面積比が \(5:4\) であるとき, \(a\) の値を求めよ。
(3) \(a\) が (2) で求めた値であるとき, \(\angle ADB=\dfrac{\pi}{2}\) であることを示せ。また, △\(ABD\) の外接円の中心と半径を求めよ。
方針
ネタバレ注意
(1)直線 \(l_1\) と円 \(C\) の接点を \((s,t)\) とおいて \(2\) つの式を立式する。
(2)\(l_1\) 同様に \(l_2\) の方程式も求める。\(l_1\) と \(l_2\) を連立することで \(H\) の \(x\) 座標が求められる。△\(BDH\) と △\(ADH\) は高さが等しいので面積の比は底辺の比と等しくなる。
(3) \(\angle ADB=\dfrac{\pi}{2}\) となるには \(l_1\) と \(l_2\) が直交していればよい。よって直線の直行条件を考える。また, \(\angle ADB=\dfrac{\pi}{2}\) から円周角の定理を用いると, \(AB\) が外接円の直径であることがわかる。
解答
(1)

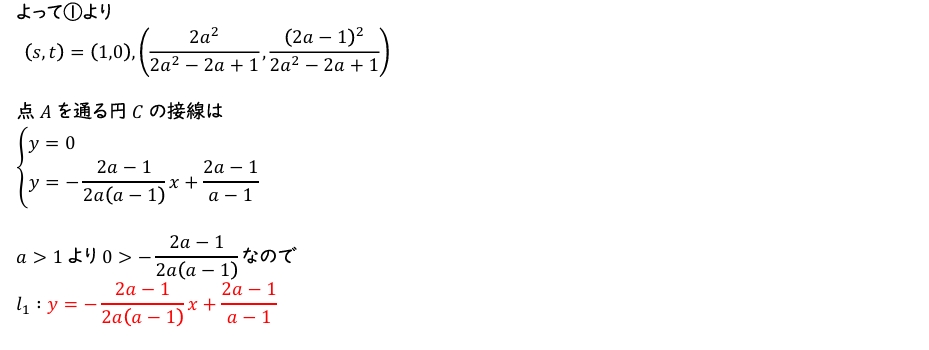
(2)



(3)



