Ⅴ
問題
\(f(x)=\dfrac{\sin(\log x)}{x}\) \((x>1)\) について以下の問いに答えよ。
(1)\(f'(x), f^”(x)\) を求めよ。
(2) \(n\) を正の整数とする。関数 \(f(x)\) が極大値をとる \(x\) で, \(e^{2(n-1)\pi}<x<e^{2n\pi}\) となるものがただ \(1\) つ存在することを示せ。また, 関数 \(f(x)\) が極小値をとる \(x\) で \(e^{2(n-1)\pi}<x<e^{2n\pi}\) となるものがただ \(1\) つ存在することを示せ。
(3)正の整数 \(n\) に対して, (2) の極大値をとる \(x\) を \(\alpha_n\), 極小値をとる \(x\) を \(\beta_n\) とする。このとき,
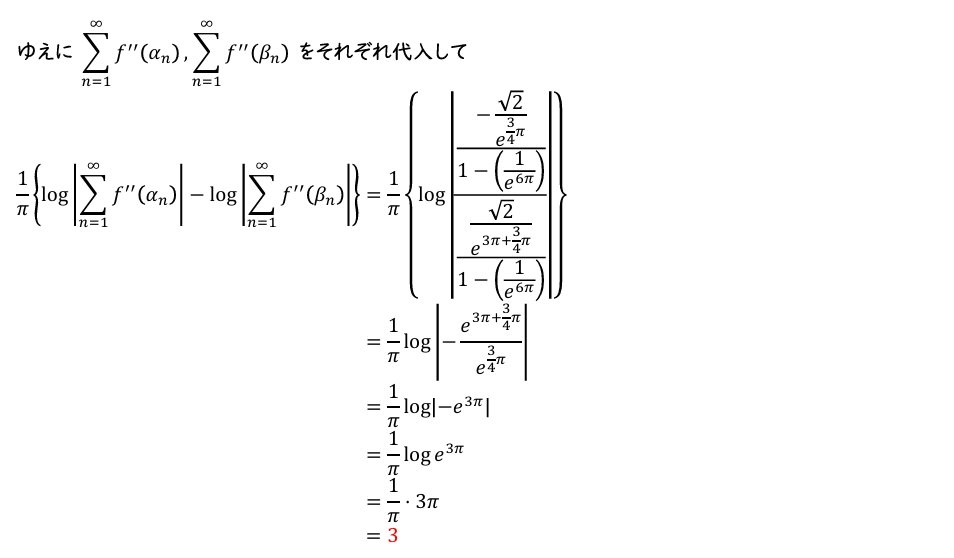
\[\dfrac{1}{\pi}\left\{\log\left|\displaystyle\sum_{n=1}^{\infty}f^{\prime\prime}(\alpha_n)\right|-\log\left|\displaystyle\sum_{n=1}^{\infty}f^{\prime\prime}(\beta_n)\right|\right\}\]は整数となる。その値を求めよ。
方針
ネタバレ注意
(1)商の微分法を利用。
(2)\(f'(x)\)を合成関数に直して増減表をつくる。
(3)\(\displaystyle\sum_{n=1}^{\infty}f^{\prime\prime}(\alpha_n)\), \(\displaystyle\sum_{n=1}^{\infty}f^{\prime\prime}(\beta_n)\) は収束する無限等比級数である。それぞれの初項と公比を求めて収束値を求める。
解答
(1)

(2)

(3)