Ⅵ
問題
\(f(x)=\sqrt{x}e^{-\frac{x^2}{4}}\) \((x\ge0)\) とし, \(\alpha=\displaystyle\int^5_0{f(x)dx}\) とする。
(1)\(f(x)\) \((x\ge0)\) が最大値をとることを示し, その値 \(M\) を求めよ。
(2) \(0\le x\le5\) において \(e^{-\frac{25}{4}}\sqrt{x}\le f(x)\) を示せ。また, \(\dfrac{10}{3}f(5)\ge\alpha\) を示せ。
(3)\(M\) は (1) で求めたものとし, 実数 \(t\) は\(\dfrac{2}{3}f(5)\le t\le M\) の範囲を動くとする。曲線 \(y=f(x)-t\) \((x\ge0)\), \(2\) 直線 \(x=0\), \(x=5\), および \(x\) 軸で囲まれた図形を, \(x\) 軸の周りに \(1\) 回転させてできる回転体の体積を \(V(t)\) とする。 \(V(t)\) の最小値を \(\alpha\) を用いて表せ。
方針
ネタバレ注意
(1)積の微分法を利用し, 増減表をかく。
(2)\(a<x<b\) において \(f(x)<g(x)\) が成り立つとき, \(\displaystyle\int^b_a{f(x)dx}<\displaystyle\int^b_a{g(x)dx}\) が成り立つ。
(3)\(x=a,x=b,y=f(x),x\) 軸で囲まれた部分を \(x\) 軸周りに回転させた回転体の体積Vは \(V=\pi\displaystyle\int^b_a\{f(x)\}^2dx\) で求められる。
解答
(1)

(2)
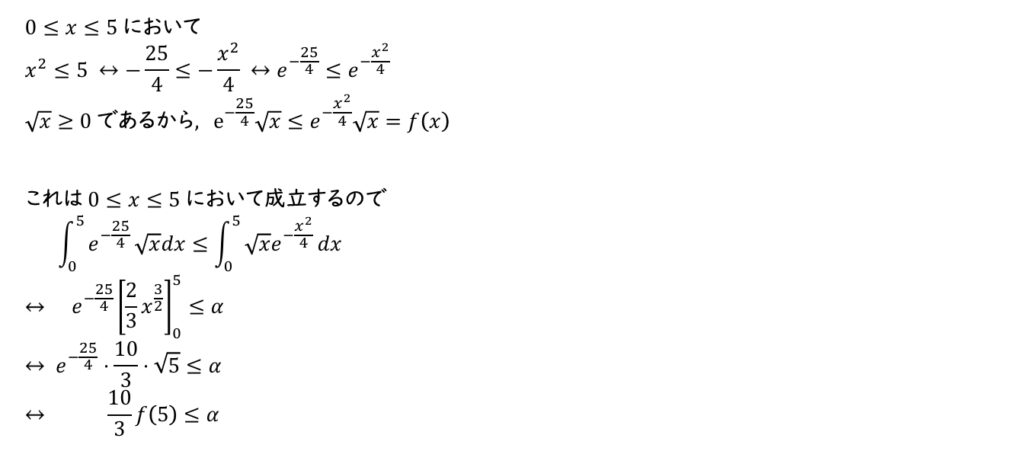
(3)




