Ⅱ
問題
\(O\) を原点とする座標空間に,3点 \(A(6,2,0)\),\(B(2,6,0)\),\(C(2,4,2)\) がある。
ベクトル \(\overrightarrow{OA}\) と\(\overrightarrow{OB}\) の内積は,\(\overrightarrow{OA}\cdot\overrightarrow{OB}=\boxed{\;\;アイ\;\;}\)である。
三角形 \(OAB\) の内角 \(\angle{AOB}\) の大きさを \(\theta\) とする。
\(\cos{\theta}=\dfrac{\boxed{ ウ }}{\boxed{ エ }}\) であり,三角形 \(OAB\) の面積は \(\boxed{\;\;オカ\;\;}\) である。
線分 \(AB\) を \(1:3\) に内分する点を \(D\) とする。
\(D\) の座標は,\(D\;(\;\boxed{ キ }\;,\boxed{ ク }\;,0)\) である。
直線 \(BC\) 上に点 \(E\) があり,\(E\) は \(\overrightarrow{OE}\cdot\overrightarrow{AB}=4\) を満たすとする。
\(r\) を実数とする。
\[\overrightarrow{OE}=\overrightarrow{OB}+r\overrightarrow{BC}\]
とすると,\(r=\dfrac{\boxed{ ケ }}{\boxed{ コ }}\) である。
点 \(C\) から \(xy\) 平面に下ろした垂線と,\(xy\) 平面の交点を \(H\) とする。直線 \(CH\) と平面 \(ODE\) の交点を \(F\) とする。
\(s\),\(t\) を実数とする。
\[\overrightarrow{OF}=s\overrightarrow{OD}+t\overrightarrow{OE}\]
とすると,\(s=\dfrac{\boxed{\;\;サシ\;\;}}{\boxed{ ス }}\),\(t=\dfrac{\boxed{\;\;セソ\;\;}}{\boxed{ タ }}\) である。\(F\) の \(z\) 座標は \(\dfrac{\boxed{\;\;チツ\;\;}}{\boxed{ テ }}\) である。
四面体 \(OABC\) の体積を \(V\) ,四面体 \(ODBF\) の体積を \(W\) とするとき,\(\dfrac{W}{V}=\dfrac{\boxed{ ト }}{\boxed{ ナ }}\) である。
方針
ネタバレ注意(クリックで表示)
ア~コ
主に内積を利用しながら基本的なベクトルの変形と成分表示の計算。
サ~テ
\(\overrightarrow{OF}\) が直線 \(CH\) 上の点でもあることに着目すると,実数 \(u\) を用いて
\(\overrightarrow{OF}=u\overrightarrow{OC}+(1-u)\overrightarrow{OH}\) とおける。
\(\overrightarrow{OF}\) について2通りの表し方ができたので,連立して \(s\),\(t\) を求める。
ト,ナ
四面体 \(OABC\) は底面が三角形 \(OAB\), 高さが \(C\) の \(z\) 座標として考えられる。同様に,四面体 \(ODBF\) においても底面を \(ODB\) ,高さが \(F\) の \(z\) 座標として考えられるのでそれぞれの体積を出して比率を考える。
解答
ネタバレ注意(クリックで表示)
\(\boxed{ ア }=2\),\(\boxed{ イ }=4\)
\(\boxed{ ウ }=3\),\(\boxed{ エ }=5\)
\(\boxed{ オ }=1\),\(\boxed{ カ }=6\)
\(\boxed{ キ }=5\),\(\boxed{ ク }=3\)
\(\boxed{ ケ }=3\),\(\boxed{ コ }=2\)
\(\boxed{ サ }=-\),\(\boxed{ シ }=2\),\(\boxed{ ス }=9\)
\(\boxed{ セ }=1\),\(\boxed{ ソ }=4\),\(\boxed{ タ }=9\)
\(\boxed{ チ }=1\),\(\boxed{ ツ }=4\),\(\boxed{ テ }=3\)
\(\boxed{ ト }=7\),\(\boxed{ ナ }=4\)
解説
ネタバレ注意(クリックで表示)
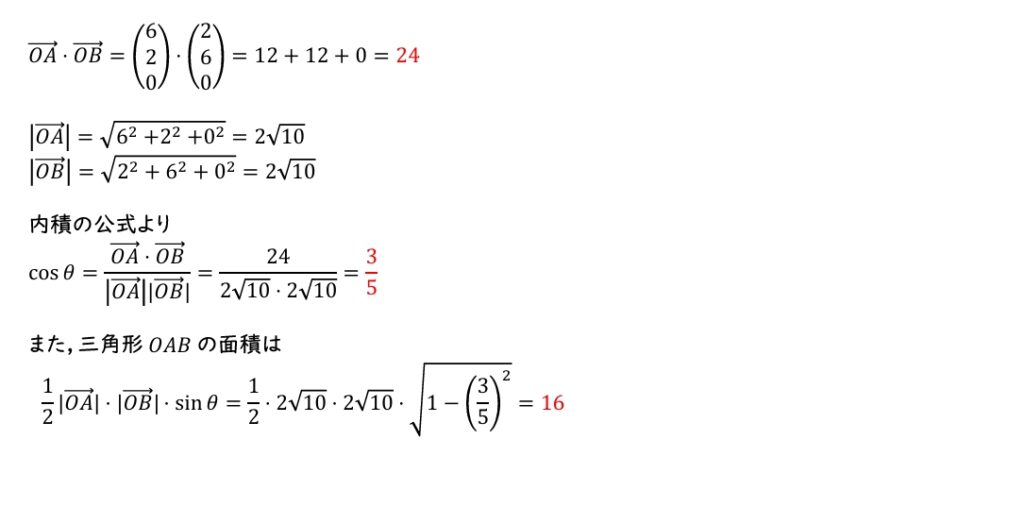
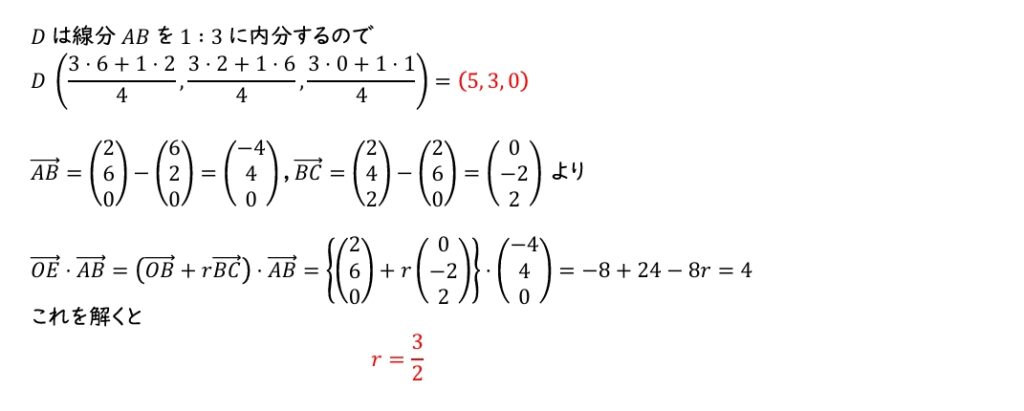


前の大問はこちら
👉️【理系数学A方式】2025年度入試 法政大学 大問1 解答解説
次の大問はこちら
👉️【理系数学A方式】2025年度入試 法政大学 大問3 解答解説
GMARCH解答解説まとめはこちら
👉️GMARCH特集|首都圏私大の王道 併願戦略の軸になるGMARCH攻略

