Ⅲ
問題
\(\alpha\),\(\beta\) を正の実数とし,\(m\),\(n\) をそれぞれ \(m>1\),\(n>1\) を満たす実数とする。\(\alpha\),\(\beta\),\(m\),\(n\) はさらに
\[2\alpha+\beta=\dfrac{\pi}{4},\tan{\alpha}=\dfrac{1}{m},\tan{\beta}=\dfrac{1}{n}\]
を満たすとする。
(1) \(n=2\) のとき,\(\cos^2{\beta}=\dfrac{\boxed{ア}}{\boxed{イ}}\),\(\cos{(2\beta)}=\dfrac{\boxed{ウ}}{\boxed{エ}}\) である。
(2) (*は選択肢省略)
加法定理より,\(\tan{\Big(\dfrac{\pi}{4}-2\alpha\Big)}=\dfrac{\boxed{オ^*}}{\boxed{カ^*}}\) である。
\(\tan{(2\alpha)}\) を \(m\) の式で表すと,\(\tan{(2\alpha)}=\dfrac{\boxed{キ^*}}{\boxed{ク^*}}\) となる。
\(\tan{\beta}=\tan{\Big(\dfrac{\pi}{4}-2\alpha\Big)}\) であるから,\(\dfrac{1}{n}\) を \(m\) の式で表すと,\(\dfrac{1}{n}=\dfrac{\boxed{ケ^*}}{\boxed{コ^*}}\) となる。
\(\boxed{コ^*}-\boxed{ケ^*}=\boxed{サ^*}\) である。
\[n=1+\dfrac{\boxed{サ^*}}{\boxed{ケ^*}} \cdot\cdot\cdot\cdot\cdot\cdot(ⅰ)\]
\(n>1\) であるから \(\boxed{サ^*}\) と \(\boxed{ケ^*}\) は同符号である。
\[\boxed{ケ^*}\;\;\boxed{シ^*}\;\;0 \cdot\cdot\cdot\cdot\cdot\cdot(ⅱ)\]
ただし,\(\boxed{シ^*}\) には不等号がはいる。
\(m>1\) であるから,不等式(ⅱ) の解は,\(m>\sqrt{\boxed{ス}}+\boxed{セ}\) である。
(3)(*は選択省略)
\(n\) が整数であるとする。
\(n\ge2\) であるから,(ⅰ)より,\(\boxed{サ^*}\;\;\boxed{ソ^*}\;\;\boxed{ケ^*}\) である。
ただし,ソは不等号がはいる。
(4) \(m>1\),\(n>1\),および(ⅰ)を満たす整数 \(m\) と整数 \(n\) の組 \((m,n)\) のうち,\(m\) が最大であるような組は \((m,n)=(\;\boxed{タ}\;,\boxed{チ}\;)\) である。
方針
ネタバレ注意(クリックで表示)
(1) \(1+\tan^2{\theta}=\dfrac{1}{\cos^2{\theta}}\),\(\tan{(\alpha+\beta)}=\dfrac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\cdot\tan{\beta}}\)
(2) (1) 同様に \(\tan\) の公式を用いて計算。
(3) \(n\ge2\) より \(n=1+\dfrac{\boxed{サ}}{\boxed{ケ}}\ge2\) を考える。
(4) (3) の不等式と(2)の不等式の解から \(m\) の範囲を考える。範囲を満たしている整数 \(m\) のうち,\(n\) も整数になるものを選ぶ。
解答
ネタバレ注意(クリックで表示)
(1)
\(\boxed{ ア }=4\),\(\boxed{ イ }=5\)
\(\boxed{ ウ }=3\),\(\boxed{ エ }=5\)
(2)
\(\boxed{ オ }=7\),\(\boxed{ カ }=8\)
\(\boxed{ キ }=2\),\(\boxed{ ク }=7\)
\(\boxed{ ケ }=6\),\(\boxed{ コ }=5\)
\(\boxed{ サ }=4\)
\(\boxed{ シ }=1\)
\(\boxed{ ス }=2\),\(\boxed{ セ }=1\)
(3)
\(\boxed{ ソ }=1\)
(4)
\(\boxed{ タ }=3\),\(\boxed{ チ }=7\)
解説
(1)ネタバレ注意(クリックで表示)
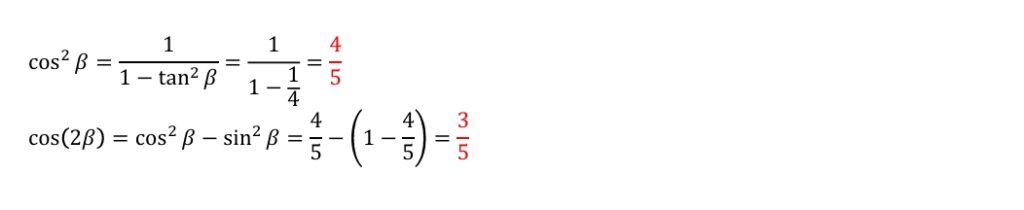
(2)ネタバレ注意(クリックで表示)

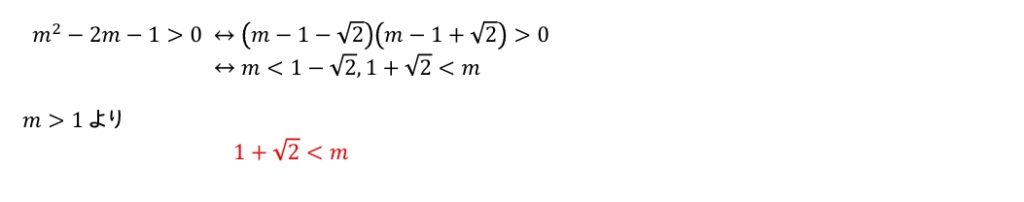
(3)ネタバレ注意(クリックで表示)
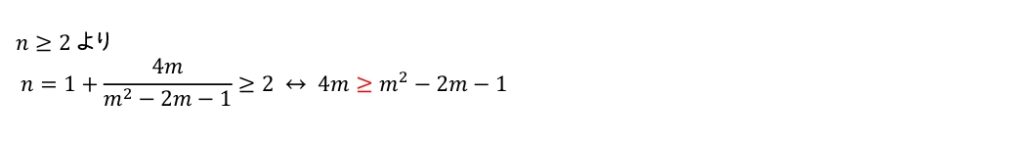
(4)ネタバレ注意(クリックで表示)
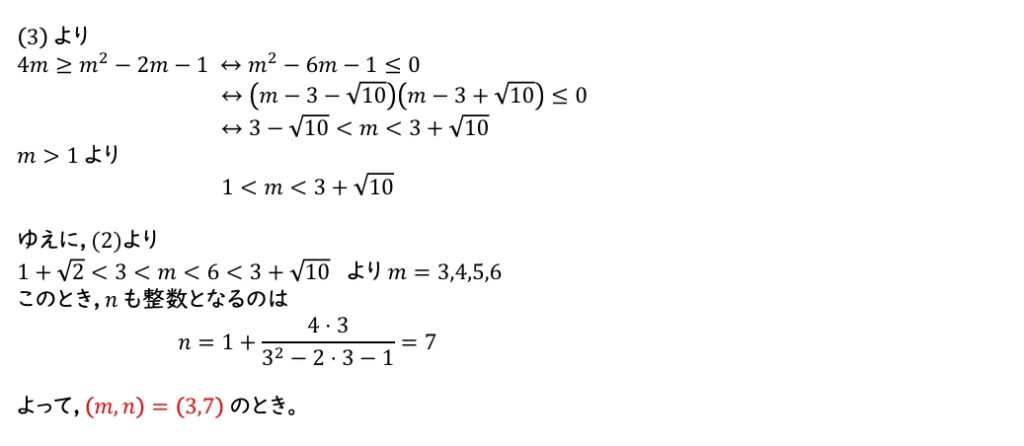
前の大問はこちら
👉️【理系数学A方式】2025年度入試 法政大学 大問2 解答解説
次の大問はこちら
👉️【理系数学A方式】2025年度入試 法政大学 大問4 解答解説(coming soon….)
GMARCH解答解説まとめはこちら
👉️GMARCH特集|首都圏私大の王道 併願戦略の軸になるGMARCH攻略

