Ⅰ
問題
複素数平面上で, 複素数\(z\)が円\(|z|=1\)の上を動くとき,\[\omega =(\frac{1+\sqrt{2}}{2})z+(\frac{1-\sqrt{2}}{2})\frac{1}{z}\]を満たす点\(\omega\)の軌跡を\(C\)とする。次の問に答えよ。
(1)\(C\)はどのような図形か, 複素数平面上に図示せよ。
(2)\(C\)と円\(|z-\frac{2+\sqrt 2}{2}|=\sqrt 2\)の共有点を求めよ。
(3)\(C\)で囲まれる領域と\(|z-\frac{2+\sqrt 2}{2}|\leq \sqrt 2\)の表す領域の共通部分の面積を求めよ。
方針
ネタバレ注意(見たい人はクリック)
(1)\(z\)について解いてみようとすると大変である。今回は\(z\)が複素数平面上の単位円を動くことから、極形式\(z=\cos\theta +i\sin\theta\)を用いて考えてみよう!
(2)複素数平面上で交点を考えることは困難であることが多いため、\(xy\)平面上で交点を考える!
(3)図形に囲まれた部分の面積を求める問題なので、(2)で出てきた結果を踏まえて積分をする!
解答
(1),(2)解答(見たい人はクリック)

(3)解答(見たい人はクリック)
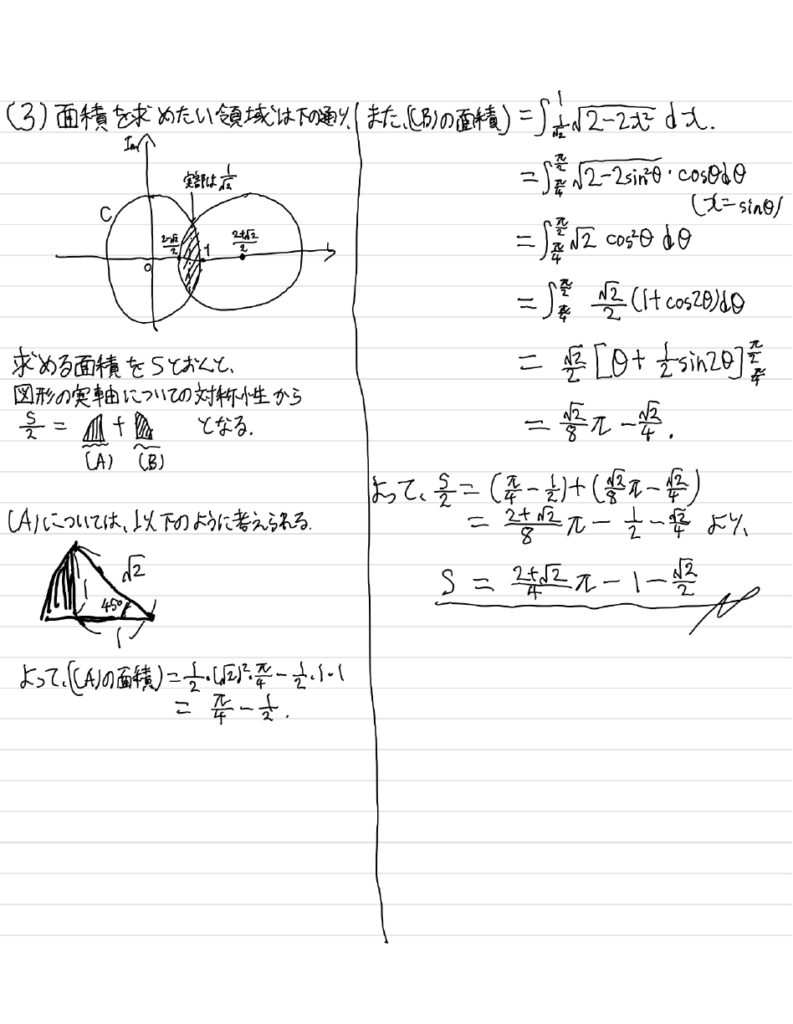
補足
ネタバレ注意(見たい人はクリック)
(3)で(A)の面積を求める際、(B)の面積を求める際の方法と同様地道に積分することでも答えを出すことができるが、上の解答のように図形的性質に気づいて計算をすれば早く答えを出すことができる。
円が絡む図形では、積分よりも図形的性質を使って面積を求められないかを考える癖を身につけよう!
Ⅱ
問題
\(xy\)平面上で, 連立不等式\(0<x\leq 1, 0\leq y\leq \log{\frac{1}{x}}\)で定まる領域と\(y\)軸の\(y\geq 0\)の部分を合わせた図形を\(D\)とする。\(D\)に含まれる三角形の面積の最大値を求めよ。
方針
ネタバレ注意(見たい人はクリック)
まず三角形の面積が最大値をとるとき、頂点の3点がすべて領域の境界上にあるのではないかと考える。
その後3頂点がどのような配置で境界上にあるのかを考え、それぞれの場合について考えて面積の最大値を求める。
また、もし等積変形に気づくことができれば調べるパターンをより少なくできる!
問題の状況を工夫や発想によってより単純なものにすることができると、難しい問題も解きやすくなる!
解答
解答

解答(続き)

補足
ネタバレ注意(見たい人はクリック)
上に用意した解答はどういった発想で書き上げられたのかがわかりにくいとは思うが、先ほど「方針」の欄でも述べたとおり「問題をより単純なものにする」といった姿勢を崩さないようにして書き上げてみたつもりでいる。
本来頂点を構成する3点は領域\(D\)内を自由に動き回っていたところを、「まず3点を領域の境界線上に固定し、次にどの境界線に何個の点があるかといった制限をかけ、最後に1辺が\(y=\log{\frac{1}{x}}\)に接するという制限を加える」といったように、段々と3点の移動範囲が狭まっていることを実感して欲しい。
Ⅲ
問題
\(1\)から\(n\)までの異なる自然数が\(1\)つずつ書かれた\(n\)枚のカードが一列に並んでいる。このとき, どのカードも現在とは異なる位置に移動するように並べ替えてでいる順列の総数を\(a_n\)で表し, 並べ方の総数\(n!\)に占める\(a_n\)の割合を\(p_n\)で表す。例えば, \(a_1=0\), \(p_1=0\), \(a_2=1\), \(p_2=\frac{1}{2}\), \(a_3=2\), \(p_3=\frac{1}{3}\)である。 次の問に答えよ。
(1) \(a_4\)の値を求めよ。
(2)\(n\geq 3\)のとき, \(a_n\)を\(a_{n-1}\)と\(a_{n-2}\)を用いて表せ。
(3)\(n\geq 2\)のとき, \(p_n-p_{n-1}\)を\(n\)を用いて表せ。
方針
ネタバレ注意(見たい人はクリック)
これは「完全順列」というものが題材となっている問題である。
(1)\(n=4\)の場合について調べるくらいであれば、地道に数え上げることができる。過不足なく数え上げるよう注意すること。
(2)これは誘導がついていないとかなり難しい。
最後の数(\(=n\))がどの位置に移動するかによって場合分けをして考える。
(3) (2)で出てきた解答を踏まえて、計算を進めてみる。
解答
(1),(2)解答

(3)解答

補足
ネタバレ注意(見たい人はクリック)
(2)の(ii)の考え方が特に初見だと難しかったのではないだろうか。
しっかりと復習して次回会ったときには解けるようにしよう。
Ⅳ
問題
空間内に原点\(O\)を中心とする半径\(r\)の球面\(S\)がある。さらに, 半径が\(1,2,3\)の球面\(S_1,S_2,S_3\)があり, これら\(4\)つの球面のうちどの\(2\)つの球面も互いに外接している。\(S_1,S_2,S_3\)の中心を順に\(P_1,P_2,P_3\)とし, \(O,P_1,P_2,P_3\)は同一平面上にないとする。さらに, 球面\(S\)が球面\(S_1,S_2,S_3\)と接する\(3\)つの点と, \(\overrightarrow{OQ}=\frac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})\)により定まる点\(Q\)は, 同一平面上にあるとする。次の問に答えよ。
(1)\(r\)の値を求めよ。
(2)四面体\(OP_1P_2P_3\)の体積を求めよ。
方針
ネタバレ注意(見たい人はクリック)
(1) \(S\)と\(S_1,S_2,S_3\)が外接する点をそれぞれ\(T_1,T_2,T_3\)とすると、これらが外接するという条件から\(\overrightarrow{OT_i}=\frac{r}{r+i}\overrightarrow{OP_i}\)となる(\(i=1,2,3\))。
4点\(Q,T_1,T_2,T_3\)が同一平面上にあるという条件から、ある実数\(s,t\)を用いて\(\overrightarrow{OQ}=s\overrightarrow{OT_1}+t\overrightarrow{OT_2}+(1-s-t)\overrightarrow{OT_3}\)となる。
これらを\(\overrightarrow{OP_1},\overrightarrow{OP_2},\overrightarrow{OP_3}\)について直して係数比較をし、\(r\)について解く。
(2) (1)の結果を用いて四面体のすべての辺の長さを求めることができる。
それを求めると、三角形\(P_1P_2P_3\)が\(\angle{P_3P_1P_2}=90^{\circ}\)となる直角三角形となることが分かる。
よって、点\(P_1\)を原点、直線\(P_1P_2\)を\(x\)軸、直線\(P_1P_3\)を\(y\)軸とする座標系を設定し、\(O(a,b,c)\)とおくことで四面体の高さ(\(=c\))を求める。
解答
解答

解答(続き)

補足
ネタバレ注意(見たい人はクリック)
(2)の方針でおそらく「点\(O\)から平面\(P_1P_2P_3\)に下ろした垂線の足を\(H\)とおき、四面体の高さ(\(=|\overrightarrow{OH}|\))を求める」という方針を立てた人は多いだろう。
しかし、今回このような方針で計算すると計算がかなり煩雑になってしまうため、その方針で進めるのは現実的に難しい。
Ⅴ
問題
\(xy\)平面上の曲線\(C: y=\sqrt[3]{x^2+2}\)を考え, \(C\)上の\((0,\sqrt[3]2)\)以外の点\(P(a,b)\)における接線を\(l: y=kx+c\)と表す。\(C\)と\(l\)の方程式から\(x\)を消去して得られる\(y\)についての3次方程式\(f(y)=0\)は\(b\)を重解としてもつので, もう1つの解を\(b’\)とする。ただし, \(b\)が3重解のときは\(b’=b\)とみなす。次の問に答えよ。
(1)\(2b+b’\)を\(k\)のみの分数式で表せ。
(2)\(b’\)を\(b\)のみの分数式で表せ。
(3)\(C\)と\(l\)の共有点で, その\(y\)座標が\(b’\)であるものを\(P'(a’,b’)\)とする。\(a\)と\(b\)が有理数ならば, \(a’\)と\(b’\)も有理数であることを示せ。
(4)\(b\)が奇数\(p,q\)と負でない整数\(r\)を用いて\(b=\frac{p}{2^rq}\)で与えられるとする。有理数\(b’\)を奇数\(p’,q’\)と整数\(s\)を用いて\(b’=\frac{p’}{2^sq’}\)と表すとき, \(s\)を\(r\)を用いて表せ。
(5)\(P(5,3)\)が曲線\(C\)上の点であることを利用して, \(C\)上に\(x\)座標と\(y\)座標がともに有理数であるような点が無数に存在することを示せ。
方針
ネタバレ注意(見たい人はクリック)
(1)方程式\(f(y)=0\)の解が(重複を除いて考えると)\(b,b,b’\)となることに注目する。
解と係数の関係により、\(2b+b'(=b+b+b’)\)が求まる!
(2) (1)で\(2b+b’\)を\(k\)を用いて表していたため、\(k\)を\(b\)で表すことができないかを考える。
その際、\(k\)が点\(P(a,b)\)での接線の傾きであったことを思い出す。
(3) (2)で求めた式を用いて考える。
(4) (2)で求めた式に\(b=\frac{p}{2^rq}\)を代入して考える。
その際、求めた式に対して各部分の偶奇をしっかりと確認する。
(5) 点\((5,3)\)を\((a,b)\)として考えて有理点\((a’,b’)\)をとり、 点\((a’,b’)\)に対して同様に有理点\((a”,b”)\)をとり、点\((a”,b”)\)に対して同様に有理点\((a”’,b”’)\)をとり、…という操作を無限に繰り返せることを証明する。
(上のような考え方は難関大でもたびたび出題されており、極限の問題でも類似の考えを用いることがある。)
その際、上のようにしてとった有理点の中で重複が生じないということも確認が必要である。
解答
解答①

解答②

補足
ネタバレ注意(見たい人はクリック)
「無数に存在する」ことの証明は慣れていない人からすると何から手をつければいいかが分からないと思うが、解法の一つに今回扱った「ある性質を満たすものを帰納的に作り出す」というものがある。
(これは覚えておくとともに、次回類題にあった際はなるべく解けるようにして欲しい。)
今回は(3),(4)を設けたことでその誘導が丁寧になされていたため、慣れている人からしたら方針は立てやすかったのではないかと思う。
総評
ネタバレ注意(見たい人はクリック)
昨年と比べて難易度が上昇しており、解き切ることが難しい大問が数多くあった。
この中でもⅠは比較的解きやすい部類の問題ではあったため、確実に得点してもらいたい。
Ⅱに関しては直感を記述に落とし込む力が試されたのではないだろうか。普段の勉強から「何となく」を言葉にする練習をしてもらいたい。
Ⅲは初見だとかなり難しい問題だったが、(1)だけは死守してもらいたい。
Ⅳ(1)は基本的な問題だが、(2)でベクトルを用いた方法以外の方針で解き進められたかで差がつく問題だったと思う。 1つの解法だけにこだわらず、「ある程度解き進めて無理そうなら別の方針で考える」といった動きを取れるようにしよう。
Ⅴは問題量が多く、試験時間内でこの問題を完答しようとすることはあまり現実的ではないが、(1)だけは死守。 また、(5)のように条件を満たすものを帰納的に作成するという考えは重要になってくるため、この問題を通して身につけてもらいたい。

