問題
複素数平面上で, 複素数\(z\)が円\(|z|=1\)の上を動くとき,\[\omega =(\frac{1+\sqrt{2}}{2})z+(\frac{1-\sqrt{2}}{2})\frac{1}{z}\]を満たす点\(\omega\)の軌跡を\(C\)とする。次の問に答えよ。
(1)\(C\)はどのような図形か, 複素数平面上に図示せよ。
(2)\(C\)と円\(|z-\frac{2+\sqrt 2}{2}|=\sqrt 2\)の共有点を求めよ。
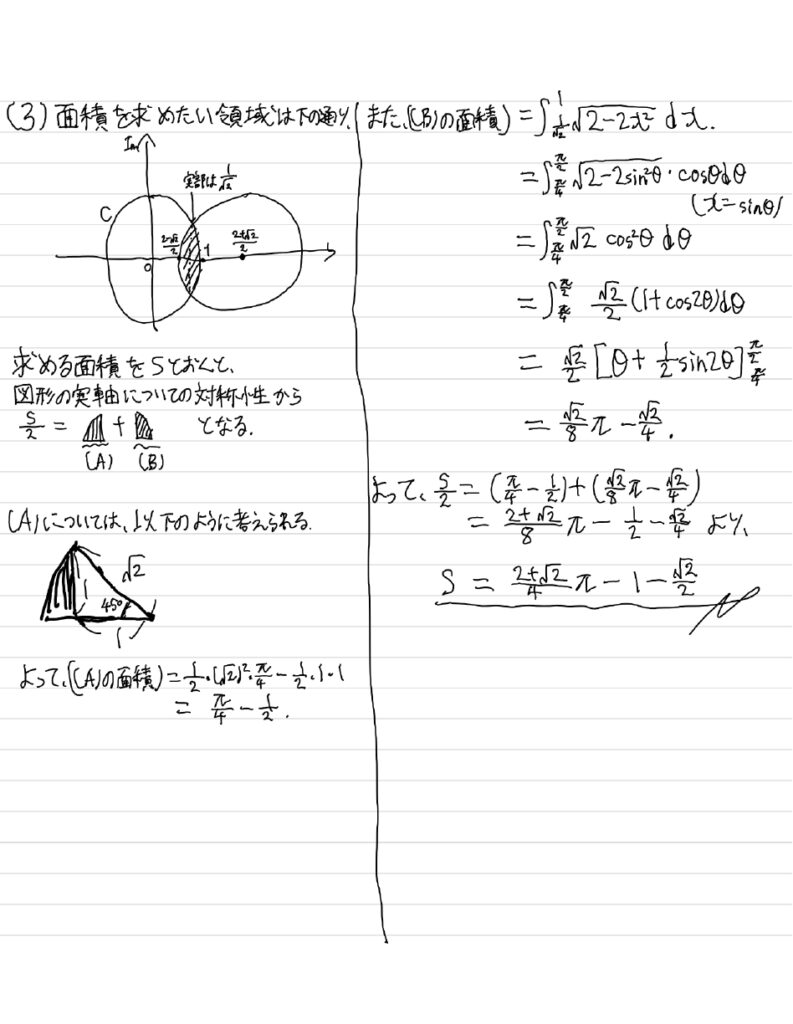
(3)\(C\)で囲まれる領域と\(|z-\frac{2+\sqrt 2}{2}|\leq \sqrt 2\)の表す領域の共通部分の面積を求めよ。
方針
前半は複素数平面についての問題であり、後半は図形の面積を求めるという積分の問題となっている。
この年の中では比較的簡単な問題なので、確実に得点を狙おう!
(1)\(z\)について解いてみようとすると大変である。今回は\(z\)が複素数平面上の単位円を動くことから、極形式\(z=\cos\theta +i\sin\theta\)を用いて考えてみよう!
(2)複素数平面上で交点を考えることは困難であることが多いため、\(xy\)平面上で交点を考える!
(3)図形に囲まれた部分の面積を求める問題なので、(2)で出てきた結果を踏まえて積分をする!
このように、必要に応じて複素数平面と\(xy\)平面を行き来できるといいですね。
解答

補足
(3)で(A)の面積を求める際、(B)の面積を求める際の方法と同様地道に積分することでも答えを出すことができるが、上の解答のように図形的性質に気づいて計算をすれば早く答えを出すことができる。
円が絡む図形では、積分よりも図形的性質を使って面積を求められないかを考える癖を身につけよう!

