Ⅰ
問題
2次方程式 \(2x^2-4bx+3ab\) が重解をもち,さらに,2次方程式 \(x^2+2(a-1)x+b+2a^2-6a-5=0\) が実数解をもつとする。ただし,\(a\) と \(b\) は実数の定数とする。
(1) \(a=5\) のとき,\(b\) の値を求めよ。
(2) \(a\) と \(b\) のそれぞれについて,とり得る値の範囲を求めよ。
(3) \(a\) と \(b\) がどちらも整数であるような組 \((a,b)\) の個数を求めよ。
方針
ネタバレ注意(クリックで表示)
(1)重解を持つときは判別式 \(D=0\),実数解を持つときは判別式 \(D\ge 0\) になる。
(2) \(2x^2-4bx+3ab=0\) は重解を持つので,判別式の条件から求められる \(b\) を場合分けして考える。
(3)(2)の解き方同様に \(b\) の値の場合分けから個数を考える。ただし,重複しているものを区別しないように注意。
解答
(1)ネタバレ注意(クリックで表示)

(2)ネタバレ注意(クリックで表示)

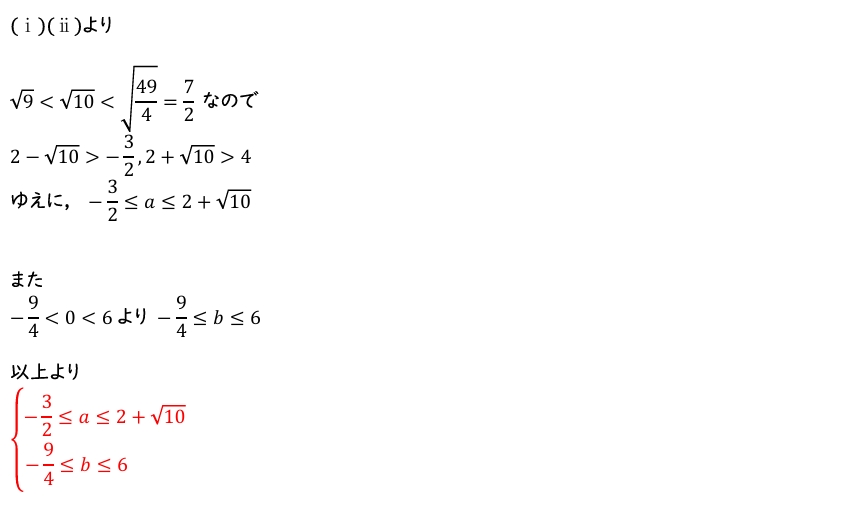
(3)ネタバレ注意(クリックで表示)

次の大問はこちら
👉️【文系数学A方式】2025年度入試 法政大学 大問2 解答解説
GMARCH解答解説まとめはこちら
👉️GMARCH特集|首都圏私大の王道 併願戦略の軸になるGMARCH攻略

