Ⅴ
問題
座標空間において4点 \(A(2, 3, 2)\),\(B(3, 7, 4)\),\(C(1, 2, 1)\),\(D(-6, 3, 20)\) をとる。
(1)\(\sin{\angle BAC}\) の値は \(\dfrac{\sqrt{\boxed{ ア }}}{\boxed{ イ }}\) である。
(2)実数 \(k,l\) に対し,ベクトル \((1, k, l)\) と平面 \(ABC\) が垂直であるとき,
\(k=\dfrac{\boxed{ ウ }}{\boxed{ エ }}\) かつ \(l=-\dfrac{\boxed{ オ }}{\boxed{ カ }}\) である。
(3) \(D\) から平面 \(ABC\) に下した垂線を \(DE\) とおく。このとき,\(E\) の座標は \((\;\boxed{ キ }\;, \;\boxed{ ク }\;, \;\boxed{ ケ }\;)\) である。
方針
ネタバレ注意(クリックで表示)
(1) △ABCにおいて \(|\overrightarrow{AB}|, \;|\overrightarrow{AC}|, \;\overrightarrow{AB}\cdot\overrightarrow{AC}\) を求め,内積の公式を考える。
(2) 平面と垂直ということは,ベクトル \((1, k, l)\) と平面上の各辺が垂直であることと等しい。つまり各辺とベクトル \((1, k, l)\) の内積は \(0\) になる。
(3) (2)同様に,内積が \(0\) になることを利用する。
解答
ネタバレ注意(クリックで表示)
(1)
\(\boxed{ ア }=2\)
\(\boxed{ イ }=3\)
(2)
\(\boxed{ ウ }=1\)
\(\boxed{ エ }=2\)
\(\boxed{ オ }=3\)
\(\boxed{ カ }=2\)
(3)
\(\boxed{ キ }=4\)
\(\boxed{ ク }=8\)
\(\boxed{ ケ }=5\)
解説
(1)ネタバレ注意(クリックで表示)
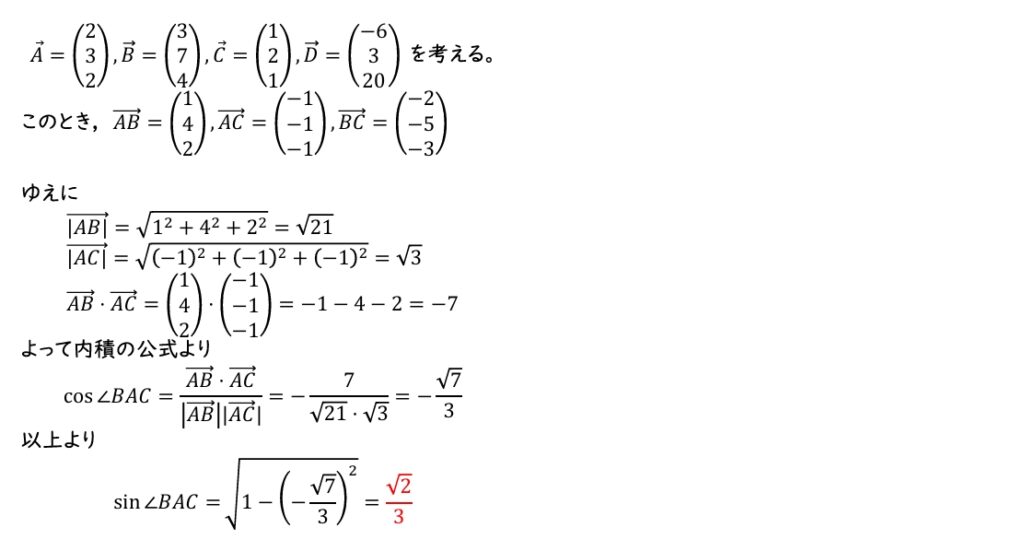
(2)ネタバレ注意(クリックで表示)

(3)ネタバレ注意(クリックで表示)

前の大問はこちら
👉️【文系数学T方式】2025年度入試 法政大学 大問4 解答解説
次の問題はこちら
👉️【文系数学T方式】2025年度入試 法政大学 大問6 解答解説
GMARCH解答解説まとめはこちら
👉️GMARCH特集|首都圏私大の王道 併願戦略の軸になるGMARCH攻略

