Ⅲ
問題
\(f(x)=3x^3-(a+1)^2x\) とおく。ただし,\(a\) は正の定数とする。
(1) 曲線 \(y=f(x)\) と \(x\) 軸で囲まれたすべての部分の面積の和が \(\dfrac{27}{2}\) となるとき,\(a\) の値を求めよ。
(2) \(f(x)\) が極大となる \(x\) の値を \(p\) とおく。\(a\) が正の実数全体を動くとき,点 \((p,f(p))\) の軌跡を図示せよ。
方針
ネタバレ注意(クリックで表示)
(1) \(x\)軸と曲線の交点を求め,積分によって面積を考える。
(2) 微分によって \(p\) の値を求め,媒介変数表示を用いて軌跡を考える。ただし,\(a\) が正であることに注意。
解答
(1)ネタバレ注意(クリックで表示)
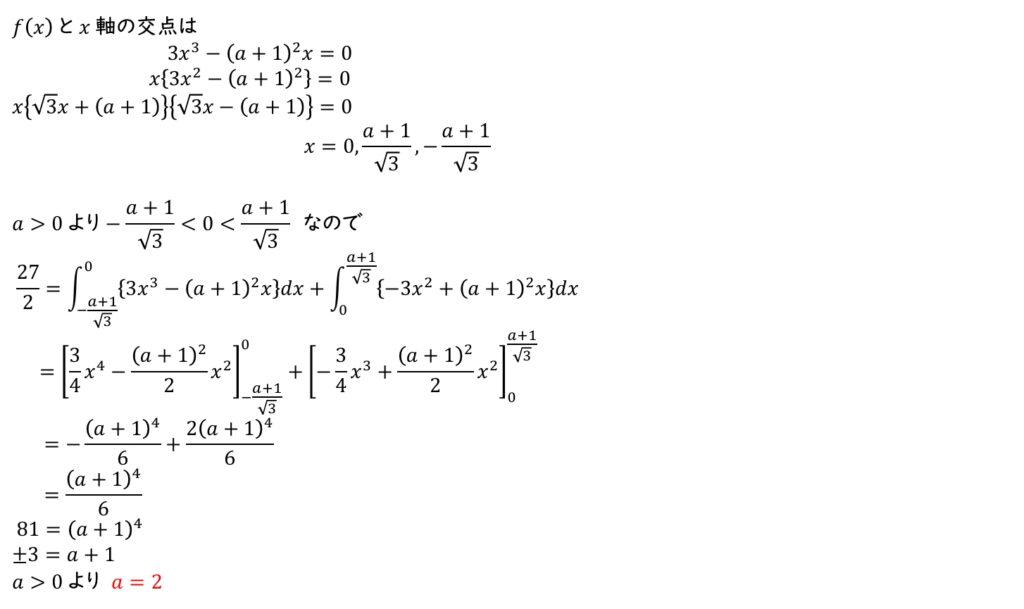
(2)ネタバレ注意(クリックで表示)
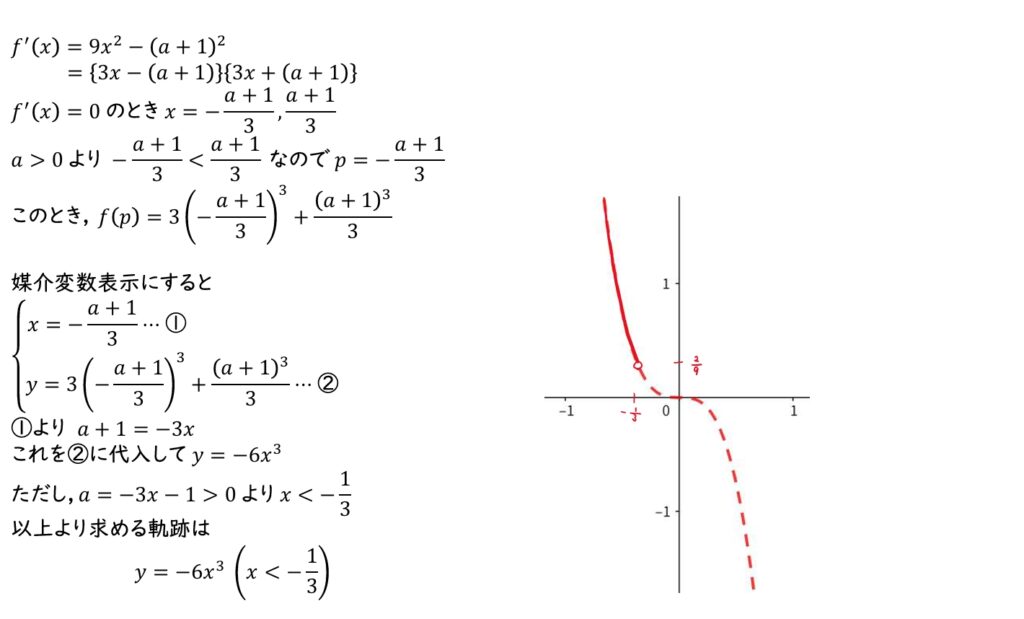
前の大問はこちら
👉️【文系数学A方式】2025年度入試 法政大学 大問2 解答解説
GMARCH解答解説まとめはこちら
👉️GMARCH特集|首都圏私大の王道 併願戦略の軸になるGMARCH攻略

