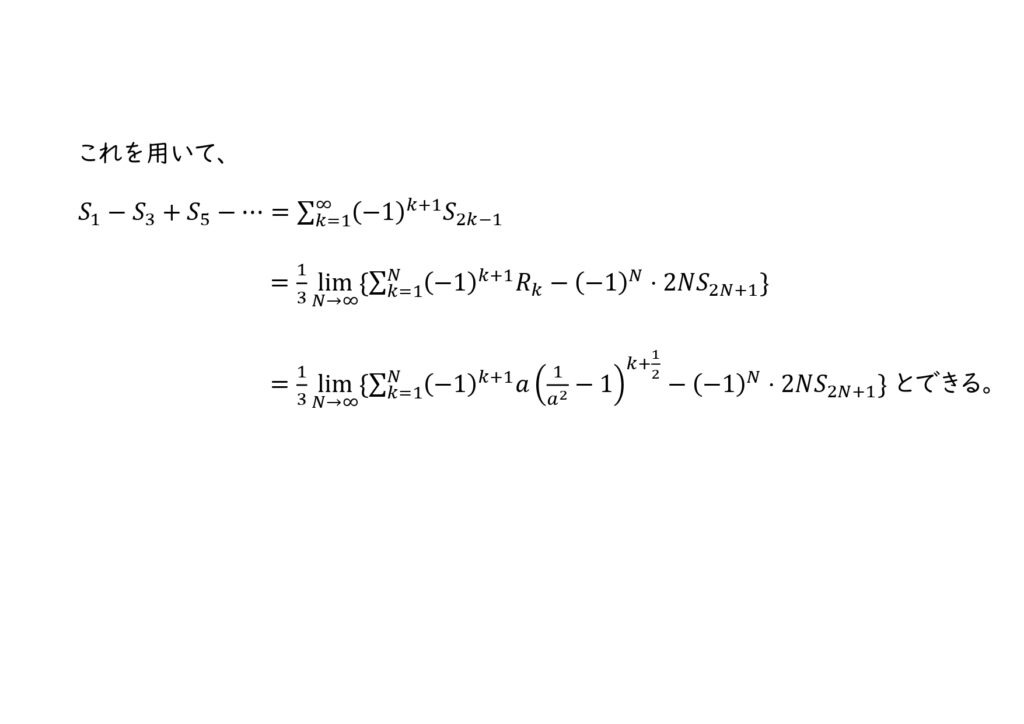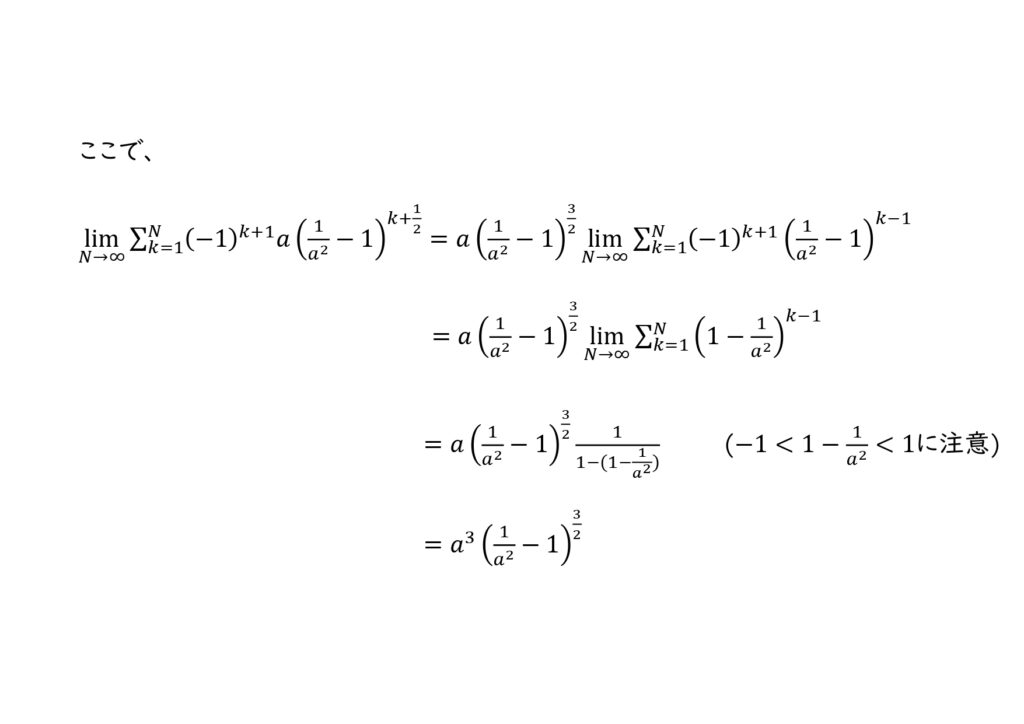Ⅱ
問題
次の問題文の空欄に最も適する答えを解答群から選び、その記号をマーク解答用紙にマークせよ。ただし、同じ記号を2度以上用いても良い。(20点)
\(a\)を\(\frac{1}{\sqrt{2}}<a<1\)を満たす定数とし、数列\(\{S_n\}\)を次で定める。
\(S_n=\int_{a}^{1} (\frac{1}{x^2}-1)^{\frac{n}{2}}\ dx\) (\(n=1,2,3,…\))
(1) \(S_{n+2}\)を部分積分法を用いて計算し、さらに\[-\int_{a}^{1} x\{(\frac{1}{x^2}-1)^{\frac{n+2}{2}}\}^{\prime}\ dx=(\boxed{ カ })S_{n+2}+(\boxed{ キ })S_n\]を用いると、次が成り立つ。\[(\boxed{ キ })S_n+(\boxed{ カ }-1)S_{n+2}=\boxed{ ク }…①\]
(2) \(S_n>0\)に注意すると、\(\frac{1}{\sqrt{2}}<a<1\)と①より、次が成り立つ。\[\lim_{n\to \infty} nS_{n+1}=\boxed{ ケ }…②\]
(3) ①の左辺に\(n=2k-1\)を代入したものを\(L_k\)とおき、右辺に同様に\(n=2k-1\)を代入したものを\(R_k\)とおく。\(N\)を自然数とすると、\[\sum_{k=1}^{N} (-1)^{k+1}L_k=(\boxed{ コ })\sum_{k=1}^{N} (-1)^{k+1}S_{2k-1}+(\boxed{ サ })S_{2N+1}\]となる。これと①,②より、以下を得る。
\(S_1-S_3+S_5-…\)
\(=\sum_{k=1}^{\infty} (-1)^{k+1}S_{2k-1}\)
\(=\frac{1}{\boxed{ コ }}\lim_{N\to \infty}\{\sum_{k=1}^N (-1)^{k+1}R_k – (\boxed{ サ })S_{2N+1}\}\)
\(=\boxed{ シ }\)
(解答選択肢は割愛)
方針
ネタバレ注意 (クリックで表示)
(1)カ、キ: \(-\int_{a}^{1} x\{(\frac{1}{x^2}-1)^{\frac{n+2}{2}}\}^{\prime}\ dx\)を部分積分を使って解こうとしても、結局もとの\(S_{n+2}\)が出てくるだけで意味はない。
よって、中身の微分を直して計算する。
そうすると\(-(n+2)\int_{a}^{1} \frac{1}{x^2}\cdot (\frac{1}{x^2}-1)^{\frac{n}{2}} dx\)が出てくるが、これを\(-(n+2)\int_{a}^{1} \{(\frac{1}{x^2}-1)+1\}\cdot (\frac{1}{x^2}-1)^{\frac{n}{2}} dx\)と変形出来るかどうかが勝負である。
ク: 上での誘導を用いて、\(S_{n+2}\)を部分積分法を用いて計算する。
(2)ケ: ①が\((n+2)S_n+(n+1)S_{n+2}=a(\frac{1}{a^2}-1)^{\frac{n+2}{2}}\)であることは(1)で求めている。
この両辺において\(n\to \infty\)とすると、\(\frac{1}{\sqrt{2}}<a<1\)に注意すれば (右辺)\(\to 0\) (\(n\to \infty\))となる。
今、どんな自然数\(n\)についても常に\(S_n>0\)となることに注意すると、①より不等式\(0<(n+1)S_{n+2}<(n+2)S_n+(n+1)S_{n+2}\)が成り立つことが分かる。
これに対してはさみうちの原理を使うことで、\(\lim_{n\to \infty} (n+1)S_{n+2}=\lim_{n\to \infty} nS_{n+1}=0\)と求められる。
(3)コ,サ: \(\sum_{k=1}^{N} (-1)^{k+1}L_k=\sum_{k=1}^{N} (-1)^{k+1}\{(2k+1)S_{2k-1}+2kS_{2k+1}\}\) となる。
\(S_3,S_5,…,S_{2N-1}\)については上の\(\Sigma\)で2回ずつ現れることから、これをまとめることで整理する。
シ: 上のコ,サで求めた式を\(\sum_{k=1}^{\infty} (-1)^{k+1}S_{2k-1}=\) の形に直すことで、\(S_1-S_3+S_5-…=\frac{1}{3}\lim_{N\to \infty} \{\sum_{k=1}^{N} (-1)^{k+1}R_k -(-1)^{N+1}2NS_{2N+1} \}\)が得られる。
{}の中身の左側は\(R_k\)を代入した後に無限等比級数の公式を、右側は(2)で求めた結果を適用することで極限が求まる。
解答
ネタバレ注意(1)カ、キ、ク (クリックで表示)
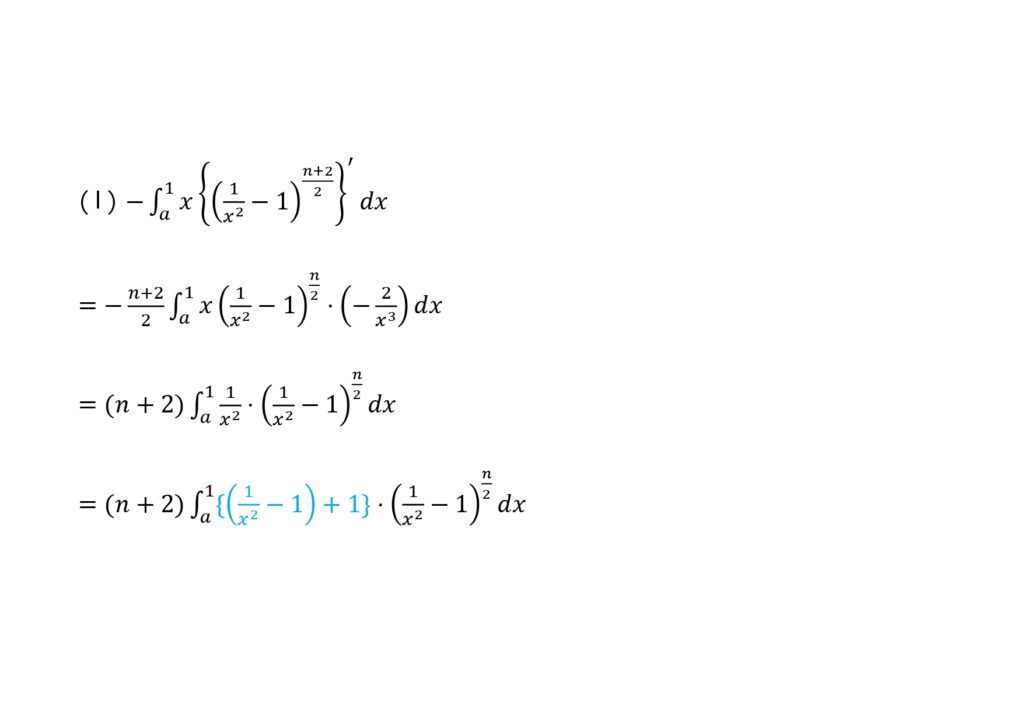


ネタバレ注意(2)ケ (クリックで表示)

ネタバレ注意(3)コ、サ、シ (クリックで表示)