Ⅳ
問題
関数 \(f(x)=\dfrac{\log{x}}{x}\) (\(x>0\)) を考える。ただし,\(log\) は自然対数を表す。以下の問いに答えよ。必要であれば,自然対数の底 \(e\) に対して,\(\displaystyle\lim_{x\to\infty}\dfrac{e^x}{x}=\infty\) を使ってもよい。
(30点)
(1) \(f(x)\) の増減を調べ,\(f(x)\) の最大値と,そのときの \(x\) の値を求めよ。
(2) 自然数 \(n\) に対して,\(a_n=\sqrt[n]{n}\) とおく。\(a_n\) の最大値と極限 \(\displaystyle\lim_{n\to\infty}a_n\) を求めよ。
(3) \(a<b\) となる自然数の組 \((a,b)\) で,\(a^b=b^a\) を満たすものをすべて答えよ。
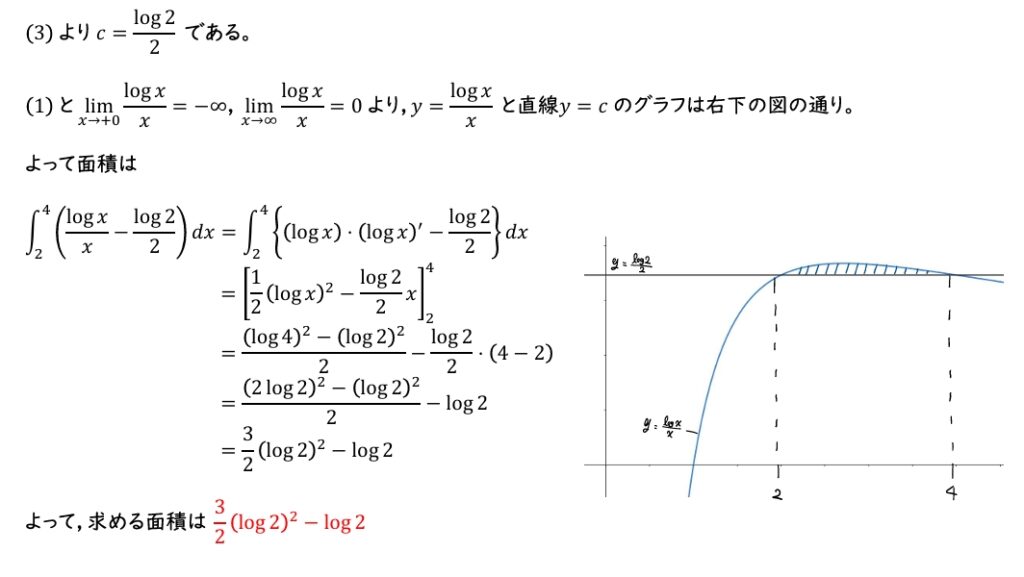
(4) (3) で求めた組 \((a,b)\) に対して,\(c=\dfrac{\log a}{a}\) とおく。\(y=\dfrac{\log x}{x}\) のグラフと直線 \(y=c\) で囲まれた部分の面積を求めよ。
方針
ネタバレ注意 (クリックで表示)
(1) \(f(x)\) を商の微分法を用いて微分すると \(f'(x)=\dfrac{1-\log{x}}{x^2}\) となる。\(f'(x)=0\) になる \(x\) の値を求めて,\(x>0\) の増減表を考える。
(2) \(n\) は自然数なので, \(a_n=\sqrt[n]{n}\) が最大となるのは \(\log{a_n}=\dfrac{\log{n}}{n}\) が最大となるときに等しい。また,\(\displaystyle\lim_{n\to\infty}a_n\) も\(\log{n}=t\) とおいて,\(\displaystyle\lim_{n\to\infty}\log{a_n}\) について考える。
(3) \(a,b\) は自然数なので,\(a^b=b^a\) ⇔ \(b\log{a}=a\log{b}\) ⇔ \(f(a)=f(b)\) となる。
(4) (3) より \(c=\dfrac{\log{2}}{2}\) である。\(f(x)\) と \(y=c\) の関係をグラフを用いて考え,積分で面積を求める。
解答
ネタバレ注意(1) (クリックで表示)

ネタバレ注意(2) (クリックで表示)

ネタバレ注意(3) (クリックで表示)

ネタバレ注意(4) (クリックで表示)