【文系数学T方式】2025年度入試法政大学大問6 解答解説

2026-01-312026-02-06

Ⅵ

問題

放物線 \(y=-\dfrac{1}{4}x^2+x+\dfrac{9}{4}\) の \(y\ge 0\) の部分を \(C\) とおく。また，\(C\) 上で \(x\) 座標が \(3\) である点を \(P\) とおき，\(P\) における \(C\) の接線と \(P\) で直交する直線を \(l_1\) とおく。さらに，\(l_1\) と \(x\) 軸との交点を \(Q\) とおく。このとき，\(Q\) を通り傾きが負の直線 \(l_2\) と \(C\) との交点 \(R\) にたいし，\(\tan{\angle PQR}\) が値 \(\dfrac{7}{4}\) をもつとする。

(1) \(Q\) の \(x\) 座標は \(\dfrac{\boxed{　ア　}}{\boxed{　イ　}}\) である。
(2) \(l_2\) の方程式は \(y=-\dfrac{\boxed{　ウ　}}{\boxed{　エ　}}x+\dfrac{\boxed{　オ　}}{\boxed{　カ　}}\) である。
(3) \(l_1\)，\(l_2\) と \(C\) によって囲まれる部分の面積は \(\dfrac{\boxed{\;\;キク\;\;}}{\boxed{\;\;ケコ\;\;}}\) である。

方針

ネタバレ注意(クリックで表示)

(1) \(y=f(x)\) とおくと \(f'(3)\) は \(P\) における接線の傾きである。\(l_1\) はこの接線と直交するので \(l_1\) の傾きと \(P\) における接線の傾きの積は \(-1\) 。
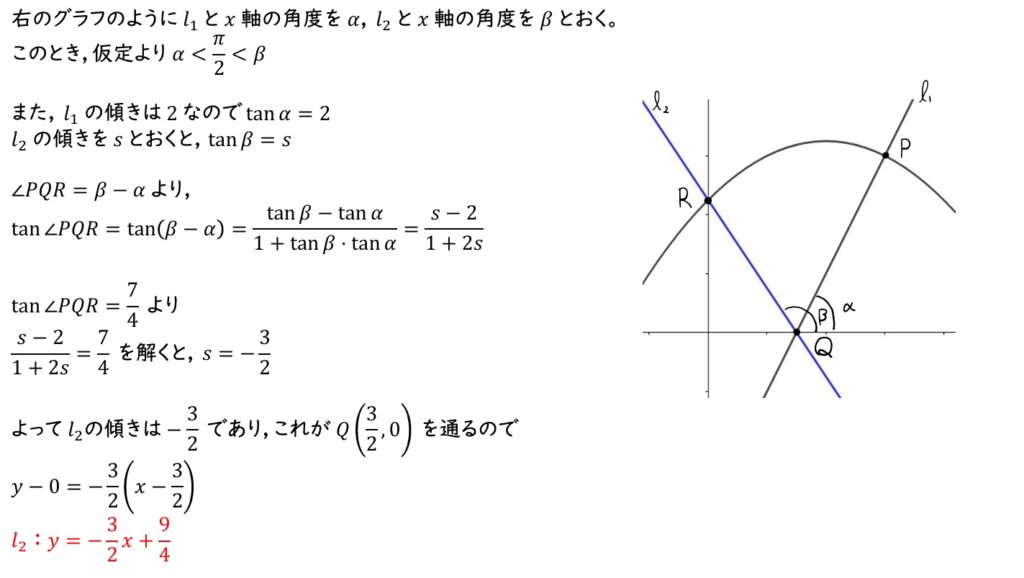
(2) \(l_1\)，\(l_2\) と \(x\) 軸の角度をそれぞれ \(\alpha\)，\(\beta\) とおく。このとき，それぞれの傾きは \(\tan{\theta}\) と等しい。また，\(\tan{\angle PQR}=\tan{(\beta-\alpha)}\) である。
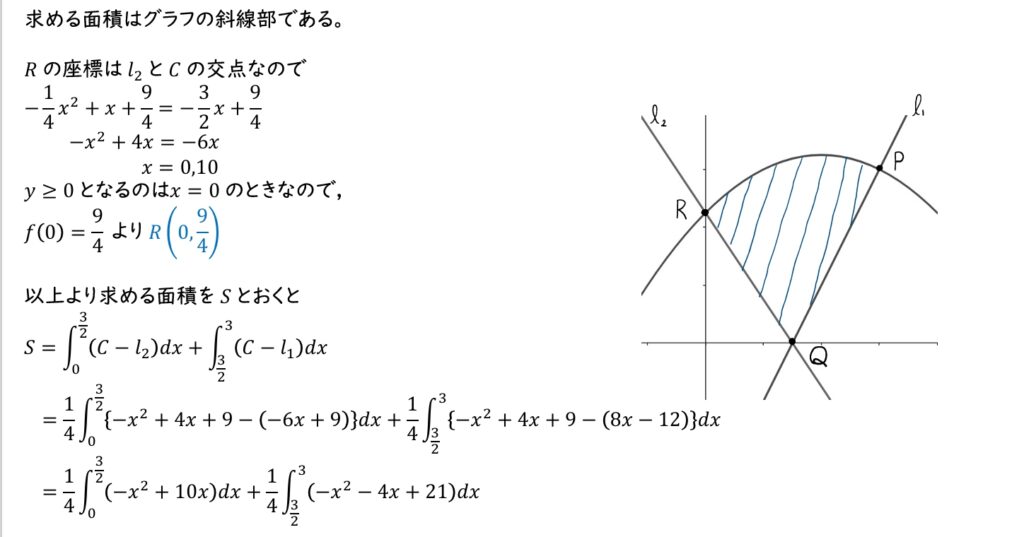
(3) (2) より \(R\) の座標が出せる。求める面積は \(\displaystyle{\int^{x_Q}_{x_R}(C-l_2)dx}+\displaystyle{\int^{x_P}_{x_Q}(C-l_1)dx}\) で計算できる。

解答

ネタバレ注意(クリックで表示)

(1)
\(\boxed{　ア　}=3\)
\(\boxed{　イ　}=2\)

(2)
\(\boxed{　ウ　}=3\)
\(\boxed{　エ　}=2\)
\(\boxed{　オ　}=9\)
\(\boxed{　カ　}=4\)

(3)
\(\boxed{　キ　}=8\)
\(\boxed{　ク　}=1\)
\(\boxed{　ケ　}=1\)
\(\boxed{　コ　}=6\)