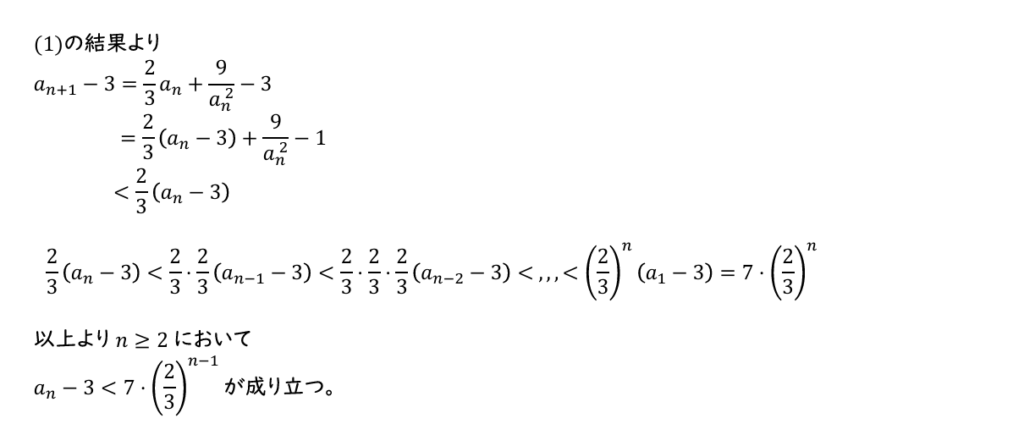Ⅳ
問題
数列{\(a_n\)}を、
\(a_1=10, a_{n+1}=\dfrac{2}{3}a_n+\dfrac{9} {a^2_n}\) \((n=1,2,3,\cdot\cdot\cdot)\)
によって定める。このとき、以下の問いに答えよ。
(1)すべての自然数\(n\)に対して\(a_n>3\)が成り立つことを示せ。
(2)すべての自然数\(n\)に対して\(a_{n+1}<a_n\)が成り立つことを示せ。
(3)\(2\)以上のすべての自然数\(n\)に対して
\(a_n-3<7\cdot\left(\dfrac{2}{3}\right)^{n-1}\)
が成り立つことを示せ。
方針
ネタバレ注意
(1)帰納法を用いて証明してみよう。
(2)\(a_{n+1}-a_n\)の符号を調べよう。
(3)(1)の結果を用いて\(a_{n+1}-3\)を\(\dfrac{2}{3}(a_n-3)\)と比較してみよう。
解答
(1)

(2)

(3)