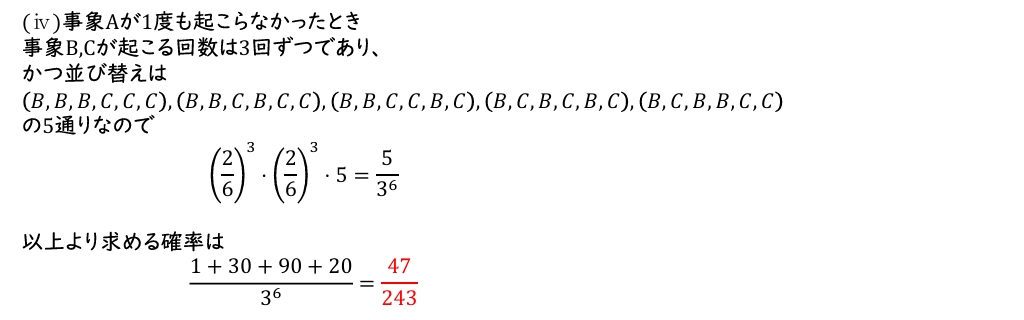Ⅴ
問題
さいころを投げて座標平面上の点\(P\)を動かす試行を繰り返す。最初の点\(P\)の位置は原点であるとする。\(1\)回の試行では\(1\)個のさいころ投げて、出た目に応じて以下の規則により点\(P\)を動かす。
・\(1\)または\(2\)が出れば、点\(P\)を\(x\)軸方向に\(+1\)だけ動かす。
・\(3\)または\(4\)が出れば、点\(P\)を\(y\)軸方向に\(+1\)だけ動かす。
・\(5\)または\(6\)が出れば、点\(P\)を\(y\)軸方向に\(-1\)だけ動かす。
\(n\)回目の試行直後の点\(P\)の座標を(\(x_n,y_n\))とする。このとき、以下の問いに答えよ。
(1)\(x_6=y_6=0\)となる確率を求めよ。
(2)\(y_6=0\)となる確率を求めよ。
(3)\(y_1,\cdot\cdot\cdot,y_5\)がすべて\(0\)以上で、かつ\(y_6=0\)となる確率を求めよ。
方針
ネタバレ注意
(1)\(x_6=y_6=0\)となるには、点が\(x\)軸方向には移動せず、\(y\)軸の正方向と負方向に同じ回数だけ移動する必要がある。
(2)\(y\)軸の正方向と負方向に同じ回数だけ移動するときを場合分けして考えてみよう。
(3)(2)の逆を場合分けして考えてみよう。
解答
(1)

(2)


(3)