Ⅵ
問題
座標平面上に、曲線\(D:y=\log{x} (x>0)\)とその上の点\(A(a,\log{a})\)がある。半径\(r\)の円\(C\)は\(y\)軸に接し、かつ円\(C\)は曲線\(D\)と点\(A\)で同一の接線を持つ。さらに、\(r<a\)が成り立つとする。このとき、以下の問いに答えよ。
(1)\(r\)を\(a\)を用いて表せ。
(2)\(r>\dfrac{a}{2}\)となることを示せ。
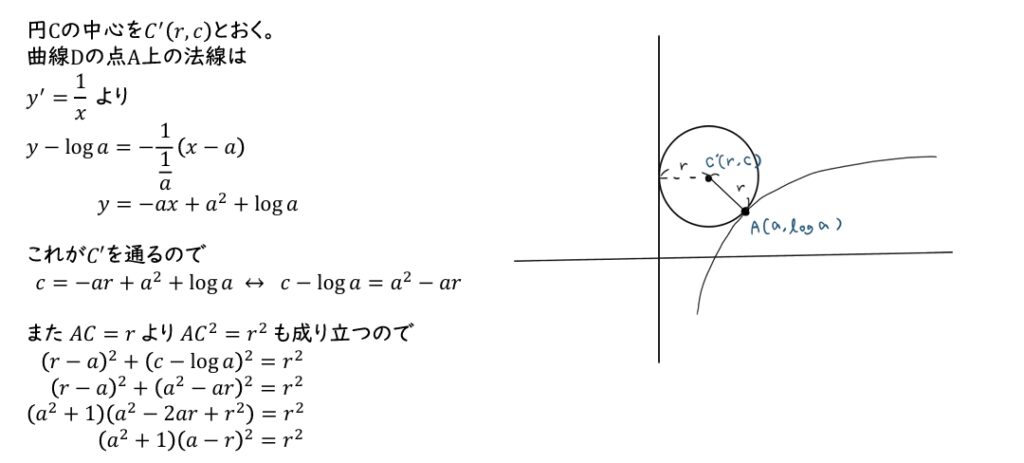
(3)\(a=\sqrt{3}\)のとき、\(x\)軸、\(y\)軸、円\(C\)の下半分と曲線\(D\)によって囲まれる領域の面積を求めよ。
方針
ネタバレ注意
(3)直接面積を求めることが難しいので、求める面積を含む五角形から必要のない面積を引いて考えてみよう。
解答
(1)

(2)
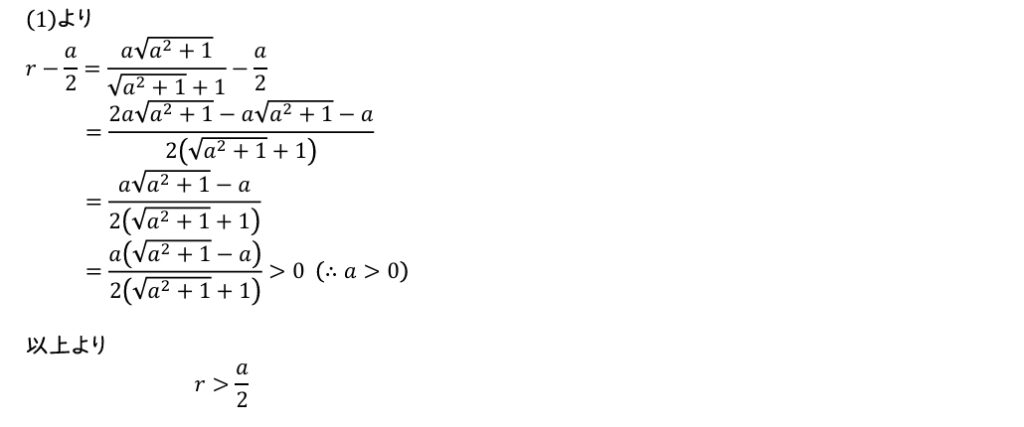
(3)