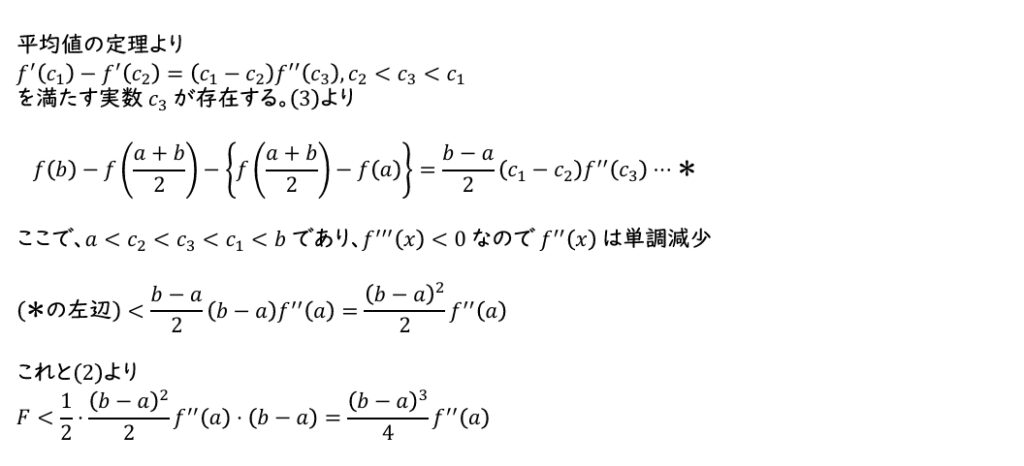Ⅸ
問題
関数\(f(x)\)は\(3\)次導関数\(f^{\prime\prime\prime}(x)\)を持ち、\(f'(0)=0\)であり、すべての実数\(x\)に対して\(f^{\prime\prime}(x)>0, f^{\prime\prime\prime}(x)<0\)を満たすものとする。また、\(0<a<b\)とし、
\(F=\dfrac{f(b)+f(a)}{2}(b-a)-\displaystyle\int^b_cf(x)dx\)
とする。このとき、以下の問いに答えよ。
(1)\(F>0\)を示せ。
(2)\(F<\dfrac{1}{2}\Big\{f(a)-2f\Big(\dfrac{a+b}{2}\Big)+f(b)\Big\}(b-a)\)を示せ。
(3)\(f(a)-2f\Big(\dfrac{a+b}{2}\Big)+f(b)<\dfrac{b-a}{2}f'(b)\)を示せ。
(4)\(F<\dfrac{(b-a)^3}{4}f^{\prime\prime}(a)\)を示せ。
方針
ネタバレ注意
(1)\(F\)を\(b\)で微分した形から大小を考えてみよう。
(2)(3)(4)平均値の定理を用いる。
解答
(1)

(2)


(3)

(4)