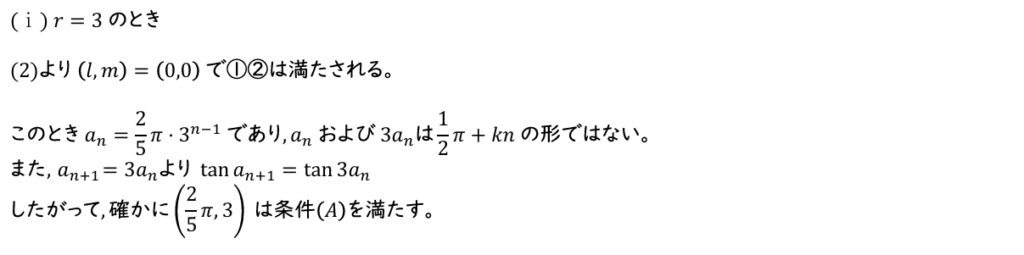Ⅰ
問題
実数の組\((a,r)\)に関する以下の条件\((A)\)を考える。
\((A)\) 初項 \(a\) ,公比 \(r\) の等比数列 \(\big\{a_n\big\}\) は,すべての正の整数 \(n\) について \(\tan a_{n+1}=\tan 3a_n\) を満たす。ただし,いずれの正の整数 \(n\) に対しても \(a_n\) および \(3a_n\) は \(\dfrac{1}{2}\pi+k\pi\) (\(k\)は整数) の形ではない。
(1)組\((a,r)\)が条件\((A)\)を満たすとき, \(\tan ar=\tan 3a\) および \(\tan ar^2=\tan 3ar\) が成り立つことを示せ。
(2)組\((a,r)\)が条件\((A)\)を満たし, かつ \(\dfrac{a}{\pi}\) が無理数であるとき, \(r=3\) であることを示せ。
(3)組 \(\Big(\dfrac{2}{5}\pi,r\Big)\)が条件\((A)\)を満たすとき, \(r\) は整数であることを示せ。
(4)\(1\le r \le 10\) を満たす \(r\) で, 組 \(\Big(\dfrac{2}{5}\pi,r\Big)\)が条件\((A)\)を満たすものをすべて求めよ。
方針
ネタバレ注意
(1)等比数列 \(\big\{a_n\big\}\) の一般項と条件 \((A)\) を比べて考える。
(2)(1)で示したものから整数 \(l,m\) を用いて \(ar\) と \(3a\) の関係, \(ar^2\) と \(3ar\) の関係をそれぞれ表し \(l=0\) のときと \(l\neq 0\) のときに分けて判定する。
(4) \(r=3\) と \(r\neq 3\) に場合分けして考える。
解答
(1)

(2)

(3)


(4)