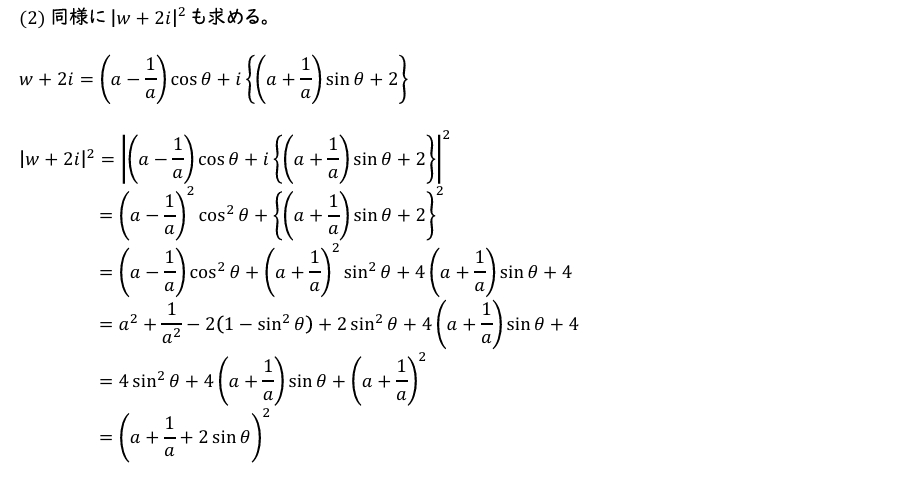Ⅳ
問題
\(i\) を虚数単位とする。\(a\) は \(1\) でない正の実数の定数とする。複素数平面において, 方程式 \(|z-a^2i|=a|z-i|\) を満たす点 \(z\) が表す図形を \(C\) とする。
(1)図形 \(C\) は原点 \(O\) を中心とする円であることを示し, その半径を求めよ。
以下の問いでは点 \(z\) は円 \(C\) 上を動くとし, \(z\) の偏角を \(\theta\) とする。ただし \(0\le\theta<2\pi\) とする。また, \(w=z-\dfrac{1}{z}\) とおく。
(2)\(|w-2i|^2\) を \(a\) と \(\sin\theta\) を用いて表せ 。
(3)\(|w-2i|+|w+2i|\) は点 \(z\) の位置によらない定数であることを示せ。
方針
ネタバレ注意
(1)原点 \(O\) を中心とする半径 \(r\) の円の方程式は \(|z|=r\)
(2)\(z=a(\cos\theta+i\sin\theta\)) とおける。これを \(w=z-\dfrac{1}{z}\) に代入して計算する。
(3)点 \(z\) の位置によらない定数, つまり \(\theta\) の値によらないことを示せばよい。(2)同様に \(|z+2i|^2\) を求めて考えてみよう。
解答
(1)

(2)
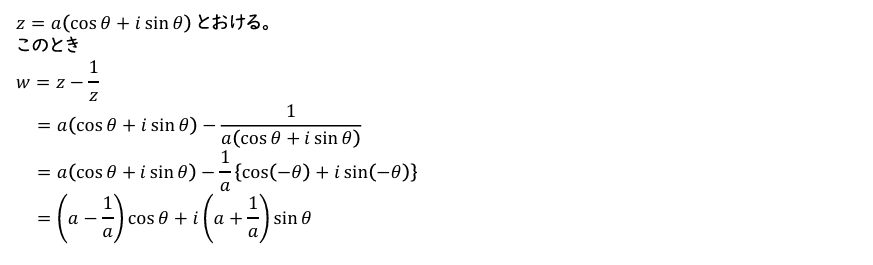
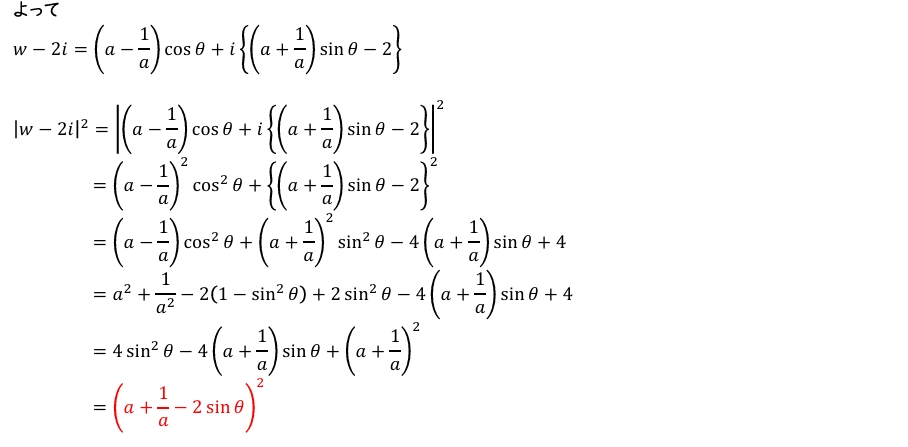
(3)