問題
立方体\(ABCD-EFGH\)を考える。辺\(AD,GH\)の中点をそれぞれ\(P,Q\)とする。辺\(AB\)を\(t:(1-t)\)に内分する点を\(R\)とする(ただし、\(0<t<1\))。\(\overrightarrow{AB}=\overrightarrow{a}, \overrightarrow{AD}=\overrightarrow{b}, \overrightarrow{AE}=\overrightarrow{c}\)と表す。いま、4点\(B,C,G,F\)を通る平面上に点\(S\)をとり、\(\overrightarrow{AS}=\alpha \overrightarrow{a}+\beta \overrightarrow{b}+\gamma \overrightarrow{c}\) (\(\alpha, \beta, \gamma\)は実数)と表す。
次の問に答えよ。
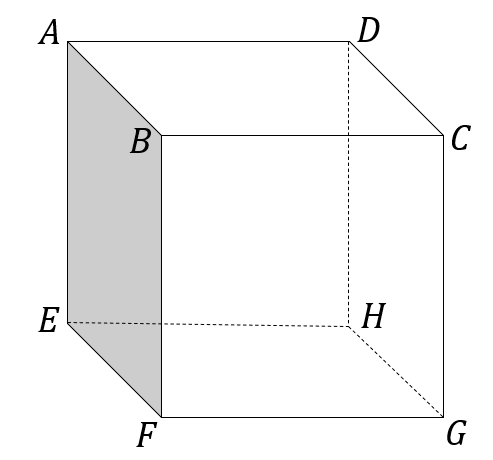
(1) \(\alpha\)を求めよ。また、\(\overrightarrow{AP}, \overrightarrow{AQ}, \overrightarrow{AR}\)をそれぞれ\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},t\)を用いて表せ。
以降、\(P,Q,R,S\)が同一平面上にあるとする。
(2) \(\beta\)を\(\gamma , t\)の式で表せ。
(3) 直線\(PS\)と直線\(QR\)が垂直に交わるとき、\(\beta, \gamma\)をそれぞれ\(t\)の式で表せ。
(4) 直線\(PS\)と直線\(QR\)が垂直に交わり、かつ点\(S\)が立方体の面\(BCGF\)上にあるとき、\(t\)のとりうる値の範囲を求めよ。
方針
(1) 図形を見ることで、これらは直ちに求めることが出来る。
(2) (1)で\(\overrightarrow{AP}, \overrightarrow{AQ}, \overrightarrow{AR}\)を求めていることから、「点\(S\)が平面\(PQR\)上にある」のように問題文を言い換えてみよう。
すると、この状況は「ある実数\(u,v\)を用いて\(\overrightarrow{AS}=u\overrightarrow{AP}+v\overrightarrow{AQ}+(1-u-v)\overrightarrow{AR}\)と表せる」のように書き換えられる。
(1)の結果を用いて\(\overrightarrow{AS}を\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)を用いて表し、\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)の一次独立性からもとの式\(\overrightarrow{AS}=\alpha \overrightarrow{a}+\beta \overrightarrow{b}+\gamma \overrightarrow{c}\)との係数比較を行う。((1)より\(\alpha =1\)であったことに注意)
(3) 内積\(\overrightarrow{PS}\cdot \overrightarrow{QR}\)が\(0\)になるという条件を使って考える。
その際、\(|\overrightarrow{a}|=|\overrightarrow{b}|=|\overrightarrow{c}|\)と、\(\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{b}\cdot \overrightarrow{c}=\overrightarrow{c}\cdot \overrightarrow{a}=0\)に注意して計算する。
(4) 点\(S\)が立方体の面\(BCGF\)上にあるというのは、\(0\leq \beta \leq 1\) かつ \(0\leq \gamma \leq 1\)であることと必要十分であることに気づく。
(3)で\(\beta ,\gamma\)を\(t\)を用いて表していることから、この式を用いて考える。
解答



